Salt melting in a saturated inclusion
Introduction
Natural fluids can sometimes high salinity. During return to surface conditions the trapped fluid can sometimes become saturated with respect to salt. A saturated inclusion is characterized by the present of a salt cube at room temperature. The inclusion is therefore 3-phase: liquid, vapour and a salt cube.
In the case of a saturated inclusion, salinity is calculated by heating the inclusion and by melting the salt cube.
Video
The video presents an inclusion saturated in sylvite (KCl). This inclusion has been choosen in a sample submitted to boiling, resulting in the production of a very-high salinity liquid phase. The experimental protocol and complete description of the results can be found in Dubois et al. (1994)[1].
Video description
The experiment starts slightly above room temperature(36°C).
At this temperature the inclusion contains three phases: liquid, vapour and a solid. This is not exactly a cube, but the geometric shape suggests a derived form of the cubic system.
All observations are made at high temperature. The sample is heated. During heating the size of the solid regularly decreases that corresponds to the dissolution of the salt crystal.
Finally the crystal totally melts at a temperature of 309.4°C. This is the salt melting temperature.
Interpretation
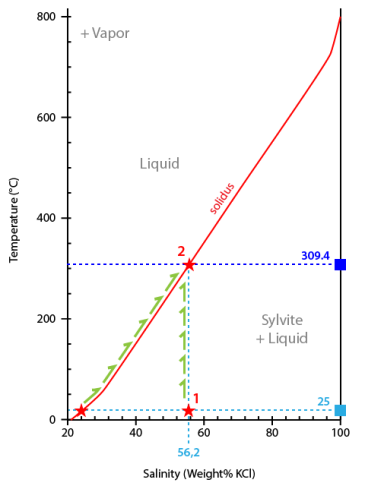
To interpret the microthermometric sequence we will use a composition-temperature diagram for the system H2O-KCl. Composition (salinity) is expressed as wt% KCl.
Salinity is determined using the above phase diagram or the empirical equation of Hall et al. (1999)[2]:
\(\textrm{wt.}\%\textrm{KCl = 21.886 + 20.28 }\Psi\textrm{ - 9.603 }\Psi^2\textrm{ + 4.078 }\Psi^3\textrm{ - 0.8724 }\Psi^4\textrm{ + 0.09174 }\Psi^5\textrm{ - 0.003776 }\Psi^6\)
\((\Psi=T°C/100, \textrm{ where }-10.7° \leq T°C \leq 770°C)\).
In the case of our video, the calculated salinity is 56.2 wt% KCl.
At 25°C the inclusion is located in the sylvite + liquid field corresponding to the observed equilibrium liquid+sylvite (in addition to vapour) (point#1).
During heating the inclusion liquid climbs along the solidus until it reaches the salt melting temperature (309.4°C) (point#2).
At this temperature the inclusion leaves the solidus and follows now a vertical line corresponding to its bull composition (56.2 wt% KCl).
More
More classically salinity in saturated inclusions are determined in the H2O-NaCl system, expressed as wt% eq. NaCl.
\(\textrm{wt.}\%\textrm{NaCl = 26.242 + 0.4928 }\Psi\textrm{ - 1.42 }\Psi^2\textrm{ - 0.223 }\Psi^3\textrm{ + 0.04129 }\Psi^4\textrm{ + 0.006295 }\Psi^5\textrm{ - 0.001967 }\Psi^6\textrm{ + 0.0001112 }\Psi^7\)
\((\Psi=T°C/100, \textrm{ where }0.1° \leq T°C \leq 801°C)\).
The empirical equation to calculate salinity can be found in Hall et al. (1999)[2]:
High salinity fluids are frequently observed in Nature. Classical geological context are environments of low-depth magmatic chambers where fluid boiling is a very common process affecting fluids.
Brines are also found at the bottom of sedimentary basins, particularly in some uranium deposits at the interface between sedimentary series and crystalline basement. These fluids are generally dominated by CaCl2.
High temperature dissolution of evaporites is another process responsible in the production of high-salinity brines with complex mixtures of numerous salts.